Pinhole Camera

In this module we have all the functions and data structures needed to describe the projection of a 3D scene space onto a 2D image plane.

In computer vision, we can map between the 3D world and a 2D image using projective geometry. The module implements the simplest camera model, the Pinhole Camera, which is the most basic model for general projective cameras from the finite cameras group.

The Pinhole Camera model is shown in the following figure:

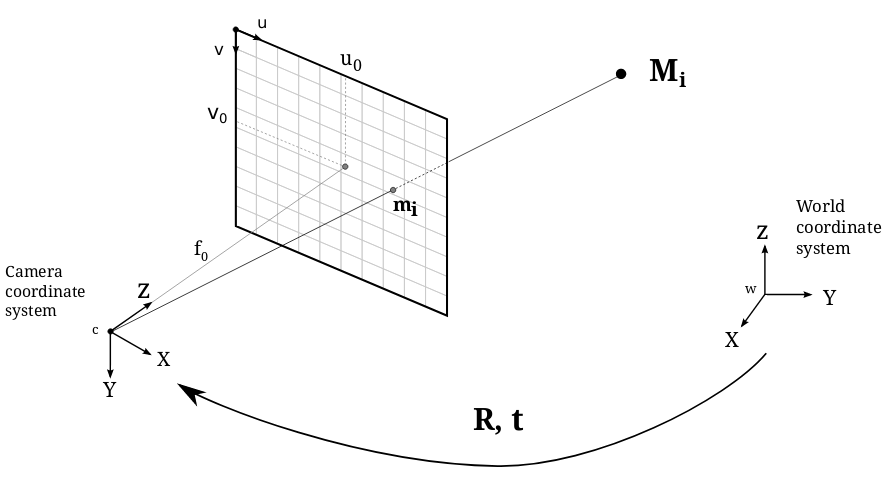
Using this model, a scene view can be formed by projecting 3D points into the image plane using a perspective transformation.

\[s \; m' = K [R|t] M'\]

or

\[\begin{split}s \begin{bmatrix} u \\ v \\ 1\end{bmatrix} = \begin{bmatrix} f_x & 0 & u_0 \\ 0 & f_y & v_0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\end{split}\]

where:

• \(M'\) is a 3D point in space with coordinates \([X,Y,Z]^T\) expressed in an Euclidean coordinate frame known as the world coordinate system.

• \(m'\) is the projection of the 3D point \(M'\) onto the image plane with coordinates \([u,v]^T\) expressed in pixel units.

• \(K\) is the camera calibration matrix, also referred as the intrinsic matrix.

• \(C\) is the principal point offset with coordinates \([u_0, v_0]^T\) at the origin in the image plane.

• \(fx, fy\) are the focal lengths expressed in pixel units.

The camera rotation and translation are expressed in terms of an Euclidean coordinate frame known as the world coordinate system. These terms are usually expressed by the joint rotation-translation matrix \([R|t]\) which is also known as the extrinsic matrix. It is used to describe the camera pose around a static scene and transforms the coordinates of a 3D point \((X,Y,Z)\) from the world coordinate system to the camera coordinate system.

The PinholeCamera expects the intrinsic matrices and the extrinsic matrices to be of shape (B, 4, 4) such that each intrinsic matrix has the following format:

\[\begin{split}\begin{bmatrix} f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

And each extrinsic matrix has the following format:

\[\begin{split}\begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

class kornia.geometry.camera.pinhole.PinholeCamera(intrinsics, extrinsics, height, width)

Class that represents a Pinhole Camera model.

Parameters:

• intrinsics (Tensor) – tensor with shape \((B, 4, 4)\) containing the full 4x4 camera calibration matrix.

• extrinsics (Tensor) – tensor with shape \((B, 4, 4)\) containing the full 4x4 rotation-translation matrix.

• height (Tensor) – tensor with shape \((B)\) containing the image height.

• width (Tensor) – tensor with shape \((B)\) containing the image width.

Note

We assume that the class attributes are in batch form in order to take advantage of PyTorch parallelism to boost computing performance.

property batch_size: int

Return the batch size of the storage.

Returns:

scalar with the batch size.

property camera_matrix: Tensor

Return the 3x3 camera matrix containing the intrinsics.

Returns:

tensor of shape \((B, 3, 3)\).

clone()

Return a deep copy of the current object instance.

Return type:

PinholeCamera

property cx: Tensor

Return the x-coordinate of the principal point.

Returns:

tensor of shape \((B)\).

property cy: Tensor

Return the y-coordinate of the principal point.

Returns:

tensor of shape \((B)\).

device()

Returns the device for camera buffers.

Return type:

device

Returns:

Device type

property extrinsics: Tensor

The full 4x4 extrinsics matrix.

Returns:

tensor of shape \((B, 4, 4)\).

property fx: Tensor

Return the focal length in the x-direction.

Returns:

tensor of shape \((B)\).

property fy: Tensor

Return the focal length in the y-direction.

Returns:

tensor of shape \((B)\).

property intrinsics: Tensor

The full 4x4 intrinsics matrix.

Returns:

tensor of shape \((B, 4, 4)\).

intrinsics_inverse()

Return the inverse of the 4x4 instrisics matrix.

Return type:

Tensor

Returns:

tensor of shape \((B, 4, 4)\).

project(point_3d)

Project a 3d point in world coordinates onto the 2d camera plane.

Parameters:

point3d – tensor containing the 3d points to be projected to the camera plane. The shape of the tensor can be \((*, 3)\).

Return type:

Tensor

Returns:

tensor of (u, v) cam coordinates with shape \((*, 2)\).

Example

>>> _ = torch.manual_seed(0)
>>> X = torch.rand(1, 3)
>>> K = torch.eye(4)[None]
>>> E = torch.eye(4)[None]
>>> h = torch.ones(1)
>>> w = torch.ones(1)
>>> pinhole = kornia.geometry.camera.PinholeCamera(K, E, h, w)
>>> pinhole.project(X)
tensor([[5.6088, 8.6827]])

property rotation_matrix: Tensor

Return the 3x3 rotation matrix from the extrinsics.

Returns:

tensor of shape \((B, 3, 3)\).

property rt_matrix: Tensor

Return the 3x4 rotation-translation matrix.

Returns:

tensor of shape \((B, 3, 4)\).

scale(scale_factor)

Scale the pinhole model.

Parameters:

scale_factor (Tensor) – a tensor with the scale factor. It has to be broadcastable with class members. The expected shape is \((B)\) or \((1)\).

Return type:

PinholeCamera

Returns:

the camera model with scaled parameters.

scale_(scale_factor)

Scale the pinhole model in-place.

Parameters:

scale_factor (Union[float, Tensor]) – a tensor with the scale factor. It has to be broadcastable with class members. The expected shape is \((B)\) or \((1)\).

Return type:

PinholeCamera

Returns:

the camera model with scaled parameters.

property translation_vector: Tensor

Return the translation vector from the extrinsics.

Returns:

tensor of shape \((B, 3, 1)\).

property tx: Tensor

Return the x-coordinate of the translation vector.

Returns:

tensor of shape \((B)\).

property ty: Tensor

Return the y-coordinate of the translation vector.

Returns:

tensor of shape \((B)\).

property tz: Tensor

Returns the z-coordinate of the translation vector.

Returns:

tensor of shape \((B)\).

unproject(point_2d, depth)

Unproject a 2d point in 3d.

Transform coordinates in the pixel frame to the world frame.

Parameters:

• point2d – tensor containing the 2d to be projected to world coordinates. The shape of the tensor can be \((*, 2)\).

• depth (Tensor) – tensor containing the depth value of each 2d points. The tensor shape must be equal to point2d \((*, 1)\).

• normalize – whether to normalize the pointcloud. This must be set to True when the depth is represented as the Euclidean ray length from the camera position.

Return type:

Tensor

Returns:

tensor of (x, y, z) world coordinates with shape \((*, 3)\).

Example

>>> _ = torch.manual_seed(0)
>>> x = torch.rand(1, 2)
>>> depth = torch.ones(1, 1)
>>> K = torch.eye(4)[None]
>>> E = torch.eye(4)[None]
>>> h = torch.ones(1)
>>> w = torch.ones(1)
>>> pinhole = kornia.geometry.camera.PinholeCamera(K, E, h, w)
>>> pinhole.unproject(x, depth)
tensor([[0.4963, 0.7682, 1.0000]])

kornia.geometry.camera.pinhole.cam2pixel(cam_coords_src, dst_proj_src, eps=1e-12)

Transform coordinates in the camera frame to the pixel frame.

Parameters:

• cam_coords – (x, y, z) coordinates defined in the first camera coordinates system. Shape must be BxHxWx3.

• dst_proj_src (Tensor) – the projection matrix between the reference and the non reference camera frame. Shape must be Bx4x4.

• eps (float, optional) – small value to avoid division by zero error. Default: 1e-12

Return type:

Tensor

Returns:

tensor of shape BxHxWx2 with (u, v) pixel coordinates.

kornia.geometry.camera.pinhole.pixel2cam(depth, intrinsics_inv, pixel_coords)

Transform coordinates in the pixel frame to the camera frame.

Parameters:

• depth (Tensor) – the source depth maps. Shape must be Bx1xHxW.

• intrinsics_inv (Tensor) – the inverse intrinsics camera matrix. Shape must be Bx4x4.

• pixel_coords (Tensor) – the grid with (u, v, 1) pixel coordinates. Shape must be BxHxWx3.

Return type:

Tensor

Returns:

tensor of shape BxHxWx3 with (x, y, z) cam coordinates.