kornia.filters#

The functions in this sections perform various image filtering operations.

Blurring#

Interactive Demo

kornia.filters.blur_pool2d(input, kernel_size, stride=2)[source]#

Compute blurs and downsample a given feature map.

See BlurPool2D for details.

See [Zha19] for more details.

Parameters

kernel_size (int) – the kernel size for max pooling..
ceil_mode – should be true to match output size of conv2d with same kernel size.

Shape:

Input: \((B, C, H, W)\)
Output: \((N, C, H_{out}, W_{out})\), where

\[H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{kernel\_size//2}[0] - \text{kernel\_size}[0]}{\text{stride}[0]} + 1\right\rfloor\]

\[W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{kernel\_size//2}[1] - \text{kernel\_size}[1]}{\text{stride}[1]} + 1\right\rfloor\]

Returns: the transformed tensor.

Note

This function is tested against https://github.com/adobe/antialiased-cnns.

Note

See a working example here.

Examples

>>> input = torch.eye(5)[None, None]
>>> blur_pool2d(input, 3)
tensor([[[[0.3125, 0.0625, 0.0000],
          [0.0625, 0.3750, 0.0625],
          [0.0000, 0.0625, 0.3125]]]])

kornia.filters.box_blur(input, kernel_size, border_type='reflect', normalized=True)[source]#

Blur an image using the box filter.

The function smooths an image using the kernel:

\[\begin{split}K = \frac{1}{\text{kernel_size}_x * \text{kernel_size}_y} \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 & 1 \\ 1 & 1 & 1 & \cdots & 1 & 1 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 1 & 1 & \cdots & 1 & 1 \\ \end{bmatrix}\end{split}\]

Parameters

image – the image to blur with shape \((B,C,H,W)\).
kernel_size (Tuple[int, int]) – the blurring kernel size.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'
normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True

Return type

Tensor

Returns

the blurred tensor with shape \((B,C,H,W)\).

Note

See a working example here.

Example

>>> input = torch.rand(2, 4, 5, 7)
>>> output = box_blur(input, (3, 3))  # 2x4x5x7
>>> output.shape
torch.Size([2, 4, 5, 7])

kornia.filters.gaussian_blur2d(input, kernel_size, sigma, border_type='reflect', separable=True)[source]#

Create an operator that blurs a tensor using a Gaussian filter.

The operator smooths the given tensor with a gaussian kernel by convolving it to each channel. It supports batched operation.

Parameters

input (Tensor) – the input tensor with shape \((B,C,H,W)\).
kernel_size (Tuple[int, int]) – the size of the kernel.
sigma (Tuple[float, float]) – the standard deviation of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'.
separable (bool, optional) – run as composition of two 1d-convolutions. Default: True

Return type

Tensor

Returns

the blurred tensor with shape \((B, C, H, W)\).

Note

See a working example here.

Examples

>>> input = torch.rand(2, 4, 5, 5)
>>> output = gaussian_blur2d(input, (3, 3), (1.5, 1.5))
>>> output.shape
torch.Size([2, 4, 5, 5])

kornia.filters.max_blur_pool2d(input, kernel_size, stride=2, max_pool_size=2, ceil_mode=False)[source]#

Compute pools and blurs and downsample a given feature map.

See MaxBlurPool2D for details.

Parameters

kernel_size (int) – the kernel size for max pooling.
stride (int, optional) – stride for pooling. Default: 2
max_pool_size (int, optional) – the kernel size for max pooling. Default: 2
ceil_mode (bool, optional) – should be true to match output size of conv2d with same kernel size. Default: False

Note

This function is tested against https://github.com/adobe/antialiased-cnns.

Note

See a working example here.

Examples

>>> input = torch.eye(5)[None, None]
>>> max_blur_pool2d(input, 3)
tensor([[[[0.5625, 0.3125],
          [0.3125, 0.8750]]]])

Return type: Tensor

kornia.filters.median_blur(input, kernel_size)[source]#

Blur an image using the median filter.

Parameters

input (Tensor) – the input image with shape \((B,C,H,W)\).
kernel_size (Tuple[int, int]) – the blurring kernel size.

Return type

Tensor

Returns

the blurred input tensor with shape \((B,C,H,W)\).

Note

See a working example here.

Example

>>> input = torch.rand(2, 4, 5, 7)
>>> output = median_blur(input, (3, 3))
>>> output.shape
torch.Size([2, 4, 5, 7])

kornia.filters.motion_blur(input, kernel_size, angle, direction, border_type='constant', mode='nearest')[source]#

Perform motion blur on tensor images.

Parameters

input (Tensor) – the input tensor with shape \((B, C, H, W)\).
kernel_size (int) – motion kernel width and height. It should be odd and positive.
angle (Union[torch.Tensor, float]) – angle of the motion blur in degrees (anti-clockwise rotation). If tensor, it must be \((B,)\).
direction (Union[float, Tensor]) – forward/backward direction of the motion blur. Lower values towards -1.0 will point the motion blur towards the back (with angle provided via angle), while higher values towards 1.0 will point the motion blur forward. A value of 0.0 leads to a uniformly (but still angled) motion blur. If tensor, it must be \((B,)\).
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'constant'.
mode (str, optional) – interpolation mode for rotating the kernel. 'bilinear' or 'nearest'. Default: 'nearest'

Return type

Tensor

Returns

the blurred image with shape \((B, C, H, W)\).

Example

>>> input = torch.randn(1, 3, 80, 90).repeat(2, 1, 1, 1)
>>> # perform exact motion blur across the batch
>>> out_1 = motion_blur(input, 5, 90., 1)
>>> torch.allclose(out_1[0], out_1[1])
True
>>> # perform element-wise motion blur across the batch
>>> out_1 = motion_blur(input, 5, torch.tensor([90., 180,]), torch.tensor([1., -1.]))
>>> torch.allclose(out_1[0], out_1[1])
False

kornia.filters.unsharp_mask(input, kernel_size, sigma, border_type='reflect')[source]#

Create an operator that sharpens a tensor by applying operation out = 2 * image - gaussian_blur2d(image).

Parameters

input (Tensor) – the input tensor with shape \((B,C,H,W)\).
kernel_size (Tuple[int, int]) – the size of the kernel.
sigma (Tuple[float, float]) – the standard deviation of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'

Return type

Tensor

Returns

the blurred tensor with shape \((B,C,H,W)\).

Examples

>>> input = torch.rand(2, 4, 5, 5)
>>> output = unsharp_mask(input, (3, 3), (1.5, 1.5))
>>> output.shape
torch.Size([2, 4, 5, 5])

Edge detection#

Interactive Demo

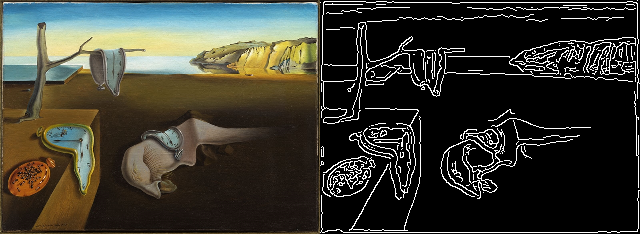
kornia.filters.canny(input, low_threshold=0.1, high_threshold=0.2, kernel_size=(5, 5), sigma=(1, 1), hysteresis=True, eps=1e-06)[source]#

Find edges of the input image and filters them using the Canny algorithm.

Parameters

input (Tensor) – input image tensor with shape \((B,C,H,W)\).
low_threshold (float, optional) – lower threshold for the hysteresis procedure. Default: 0.1
high_threshold (float, optional) – upper threshold for the hysteresis procedure. Default: 0.2
kernel_size (Tuple[int, int], optional) – the size of the kernel for the gaussian blur. Default: (5, 5)
sigma (Tuple[float, float], optional) – the standard deviation of the kernel for the gaussian blur. Default: (1, 1)
hysteresis (bool, optional) – if True, applies the hysteresis edge tracking. Otherwise, the edges are divided between weak (0.5) and strong (1) edges. Default: True
eps (float, optional) – regularization number to avoid NaN during backprop. Default: 1e-06

Return type

Tuple[Tensor, Tensor]

Returns

the canny edge magnitudes map, shape of \((B,1,H,W)\).
the canny edge detection filtered by thresholds and hysteresis, shape of \((B,1,H,W)\).

Note

See a working example here.

Example

>>> input = torch.rand(5, 3, 4, 4)
>>> magnitude, edges = canny(input)  # 5x3x4x4
>>> magnitude.shape
torch.Size([5, 1, 4, 4])
>>> edges.shape
torch.Size([5, 1, 4, 4])

kornia.filters.laplacian(input, kernel_size, border_type='reflect', normalized=True)[source]#

Create an operator that returns a tensor using a Laplacian filter.

The operator smooths the given tensor with a laplacian kernel by convolving it to each channel. It supports batched operation.

Parameters

input (Tensor) – the input image tensor with shape \((B, C, H, W)\).
kernel_size (int) – the size of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'
normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True

Return type

Tensor

Returns

the blurred image with shape \((B, C, H, W)\).

Note

See a working example here.

Examples

>>> input = torch.rand(2, 4, 5, 5)
>>> output = laplacian(input, 3)
>>> output.shape
torch.Size([2, 4, 5, 5])

kornia.filters.sobel(input, normalized=True, eps=1e-06)[source]#

Compute the Sobel operator and returns the magnitude per channel.

Parameters

input (Tensor) – the input image with shape \((B,C,H,W)\).
normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True
eps (float, optional) – regularization number to avoid NaN during backprop. Default: 1e-06

Return type

Tensor

Returns

the sobel edge gradient magnitudes map with shape \((B,C,H,W)\).

Note

See a working example here.

Example

>>> input = torch.rand(1, 3, 4, 4)
>>> output = sobel(input)  # 1x3x4x4
>>> output.shape
torch.Size([1, 3, 4, 4])

kornia.filters.spatial_gradient(input, mode='sobel', order=1, normalized=True)[source]#

Compute the first order image derivative in both x and y using a Sobel operator.

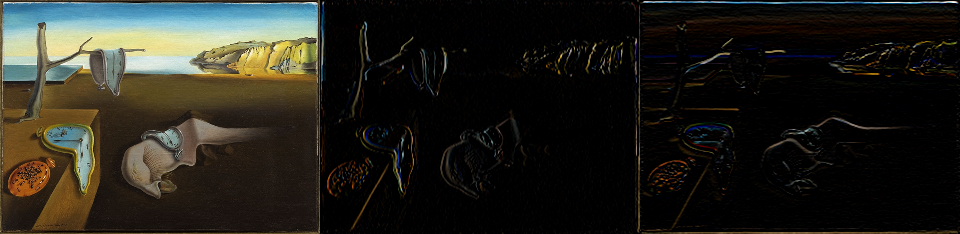
Parameters

input (Tensor) – input image tensor with shape \((B, C, H, W)\).
mode (str, optional) – derivatives modality, can be: sobel or diff. Default: 'sobel'
order (int, optional) – the order of the derivatives. Default: 1
normalized (bool, optional) – whether the output is normalized. Default: True

Return type

Tensor

Returns

the derivatives of the input feature map. with shape \((B, C, 2, H, W)\).

Note

See a working example here.

Examples

>>> input = torch.rand(1, 3, 4, 4)
>>> output = spatial_gradient(input)  # 1x3x2x4x4
>>> output.shape
torch.Size([1, 3, 2, 4, 4])

kornia.filters.spatial_gradient3d(input, mode='diff', order=1)[source]#

Compute the first and second order volume derivative in x, y and d using a diff operator.

Parameters

input (Tensor) – input features tensor with shape \((B, C, D, H, W)\).
mode (str, optional) – derivatives modality, can be: sobel or diff. Default: 'diff'
order (int, optional) – the order of the derivatives. Default: 1

Returns

(B, C, 3, D, H, W) or \((B, C, 6, D, H, W)\).

Return type

the spatial gradients of the input feature map with shape math

Examples

>>> input = torch.rand(1, 4, 2, 4, 4)
>>> output = spatial_gradient3d(input)
>>> output.shape
torch.Size([1, 4, 3, 2, 4, 4])

Filtering API#

kornia.filters.filter2d(input, kernel, border_type='reflect', normalized=False, padding='same')[source]#

Convolve a tensor with a 2d kernel.

The function applies a given kernel to a tensor. The kernel is applied independently at each depth channel of the tensor. Before applying the kernel, the function applies padding according to the specified mode so that the output remains in the same shape.

Parameters

input (Tensor) – the input tensor with shape of \((B, C, H, W)\).
kernel (Tensor) – the kernel to be convolved with the input tensor. The kernel shape must be \((1, kH, kW)\) or \((B, kH, kW)\).
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'
normalized (bool, optional) – If True, kernel will be L1 normalized. Default: False
padding (str, optional) – This defines the type of padding. 2 modes available 'same' or 'valid'. Default: 'same'

Returns

the convolved tensor of same size and numbers of channels as the input with shape \((B, C, H, W)\).

Return type

torch.Tensor

Example

>>> input = torch.tensor([[[
...    [0., 0., 0., 0., 0.],
...    [0., 0., 0., 0., 0.],
...    [0., 0., 5., 0., 0.],
...    [0., 0., 0., 0., 0.],
...    [0., 0., 0., 0., 0.],]]])
>>> kernel = torch.ones(1, 3, 3)
>>> filter2d(input, kernel, padding='same')
tensor([[[[0., 0., 0., 0., 0.],
          [0., 5., 5., 5., 0.],
          [0., 5., 5., 5., 0.],
          [0., 5., 5., 5., 0.],
          [0., 0., 0., 0., 0.]]]])

kornia.filters.filter2d_separable(input, kernel_x, kernel_y, border_type='reflect', normalized=False, padding='same')[source]#

Convolve a tensor with two 1d kernels, in x and y directions.

Parameters

input (Tensor) – the input tensor with shape of \((B, C, H, W)\).
kernel_x (Tensor) – the kernel to be convolved with the input tensor. The kernel shape must be \((1, kW)\) or \((B, kW)\).
kernel_y (Tensor) – the kernel to be convolved with the input tensor. The kernel shape must be \((1, kH)\) or \((B, kH)\).
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'
normalized (bool, optional) – If True, kernel will be L1 normalized. Default: False
padding (str, optional) – This defines the type of padding. 2 modes available 'same' or 'valid'. Default: 'same'

Returns

the convolved tensor of same size and numbers of channels as the input with shape \((B, C, H, W)\).

Return type

torch.Tensor

Example

>>> input = torch.tensor([[[
...    [0., 0., 0., 0., 0.],
...    [0., 0., 0., 0., 0.],
...    [0., 0., 5., 0., 0.],
...    [0., 0., 0., 0., 0.],
...    [0., 0., 0., 0., 0.],]]])
>>> kernel = torch.ones(1, 3)

>>> filter2d_separable(input, kernel, kernel, padding='same')
tensor([[[[0., 0., 0., 0., 0.],
          [0., 5., 5., 5., 0.],
          [0., 5., 5., 5., 0.],
          [0., 5., 5., 5., 0.],
          [0., 0., 0., 0., 0.]]]])

kornia.filters.filter3d(input, kernel, border_type='replicate', normalized=False)[source]#

Convolve a tensor with a 3d kernel.

Parameters

input (Tensor) – the input tensor with shape of \((B, C, D, H, W)\).
kernel (Tensor) – the kernel to be convolved with the input tensor. The kernel shape must be \((1, kD, kH, kW)\) or \((B, kD, kH, kW)\).
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'replicate' or 'circular'. Default: 'replicate'
normalized (bool, optional) – If True, kernel will be L1 normalized. Default: False

Return type

Tensor

Returns

the convolved tensor of same size and numbers of channels as the input with shape \((B, C, D, H, W)\).

Example

>>> input = torch.tensor([[[
...    [[0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.]],
...    [[0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 5., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.]],
...    [[0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.],
...     [0., 0., 0., 0., 0.]]
... ]]])
>>> kernel = torch.ones(1, 3, 3, 3)
>>> filter3d(input, kernel)
tensor([[[[[0., 0., 0., 0., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 0., 0., 0., 0.]],

          [[0., 0., 0., 0., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 0., 0., 0., 0.]],

          [[0., 0., 0., 0., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 5., 5., 5., 0.],
           [0., 0., 0., 0., 0.]]]]])

Kernels#

kornia.filters.get_gaussian_kernel1d(kernel_size, sigma, force_even=False)[source]#

Function that returns Gaussian filter coefficients.

Parameters

kernel_size (int) – filter size. It should be odd and positive.
sigma (float) – gaussian standard deviation.
force_even (bool, optional) – overrides requirement for odd kernel size. Default: False

Return type

Tensor

Returns

1D tensor with gaussian filter coefficients.

Shape:

Output: \((\text{kernel_size})\)

Examples

>>> get_gaussian_kernel1d(3, 2.5)
tensor([0.3243, 0.3513, 0.3243])

>>> get_gaussian_kernel1d(5, 1.5)
tensor([0.1201, 0.2339, 0.2921, 0.2339, 0.1201])

kornia.filters.get_gaussian_erf_kernel1d(kernel_size, sigma, force_even=False)[source]#

Function that returns Gaussian filter coefficients by interpolating the error function, adapted from: https://github.com/Project-MONAI/MONAI/blob/master/monai/networks/layers/convutils.py.

Parameters

kernel_size (int) – filter size. It should be odd and positive.
sigma (float) – gaussian standard deviation.
force_even (bool, optional) – overrides requirement for odd kernel size. Default: False

Return type

Tensor

Returns

1D tensor with gaussian filter coefficients.

Shape:

Output: \((\text{kernel_size})\)

Examples

>>> get_gaussian_erf_kernel1d(3, 2.5)
tensor([0.3245, 0.3511, 0.3245])

>>> get_gaussian_erf_kernel1d(5, 1.5)
tensor([0.1226, 0.2331, 0.2887, 0.2331, 0.1226])

kornia.filters.get_gaussian_discrete_kernel1d(kernel_size, sigma, force_even=False)[source]#

Function that returns Gaussian filter coefficients based on the modified Bessel functions. Adapted from: https://github.com/Project-MONAI/MONAI/blob/master/monai/networks/layers/convutils.py.

Parameters

kernel_size (int) – filter size. It should be odd and positive.
sigma (float) – gaussian standard deviation.
force_even (bool, optional) – overrides requirement for odd kernel size. Default: False

Return type

Tensor

Returns

1D tensor with gaussian filter coefficients.

Shape:

Output: \((\text{kernel_size})\)

Examples

>>> get_gaussian_discrete_kernel1d(3, 2.5)
tensor([0.3235, 0.3531, 0.3235])

>>> get_gaussian_discrete_kernel1d(5, 1.5)
tensor([0.1096, 0.2323, 0.3161, 0.2323, 0.1096])

kornia.filters.get_gaussian_kernel2d(kernel_size, sigma, force_even=False)[source]#

Function that returns Gaussian filter matrix coefficients.

Parameters

kernel_size (Tuple[int, int]) – filter sizes in the x and y direction. Sizes should be odd and positive.
sigma (Tuple[float, float]) – gaussian standard deviation in the x and y direction.
force_even (bool, optional) – overrides requirement for odd kernel size. Default: False

Return type

Tensor

Returns

2D tensor with gaussian filter matrix coefficients.

Shape:

Output: \((\text{kernel_size}_x, \text{kernel_size}_y)\)

Examples

>>> get_gaussian_kernel2d((3, 3), (1.5, 1.5))
tensor([[0.0947, 0.1183, 0.0947],
        [0.1183, 0.1478, 0.1183],
        [0.0947, 0.1183, 0.0947]])
>>> get_gaussian_kernel2d((3, 5), (1.5, 1.5))
tensor([[0.0370, 0.0720, 0.0899, 0.0720, 0.0370],
        [0.0462, 0.0899, 0.1123, 0.0899, 0.0462],
        [0.0370, 0.0720, 0.0899, 0.0720, 0.0370]])

kornia.filters.get_hanning_kernel1d(kernel_size, device=torch.device('cpu'), dtype=torch.float)[source]#

Returns Hanning (also known as Hann) kernel, used in signal processing and KCF tracker.

\[\begin{split}w(n) = 0.5 - 0.5cos\\left(\\frac{2\\pi{n}}{M-1}\\right) \\qquad 0 \\leq n \\leq M-1\end{split}\]

See further in numpy docs https://numpy.org/doc/stable/reference/generated/numpy.hanning.html

Parameters

kernel_size (int) – The size the of the kernel. It should be positive.

Return type

Tensor

Returns

1D tensor with Hanning filter coefficients.: \[\begin{split}w(n) = 0.5 - 0.5cos\\left(\\frac{2\\pi{n}}{M-1}\\right)\end{split}\]

Shape:

Output: math:(text{kernel_size})

Examples

>>> get_hanning_kernel1d(4)
tensor([0.0000, 0.7500, 0.7500, 0.0000])

kornia.filters.get_hanning_kernel2d(kernel_size, device=torch.device('cpu'), dtype=torch.float)[source]#

Returns 2d Hanning kernel, used in signal processing and KCF tracker.

Parameters

kernel_size (Tuple[int, int]) – The size of the kernel for the filter. It should be positive.

Return type

Tensor

Returns

2D tensor with Hanning filter coefficients.: \[\begin{split}w(n) = 0.5 - 0.5cos\\left(\\frac{2\\pi{n}}{M-1}\\right)\end{split}\]

Shape:

Output: math:(text{kernel_size[0], kernel_size[1]})

kornia.filters.get_laplacian_kernel1d(kernel_size)[source]#

Function that returns the coefficients of a 1D Laplacian filter.

Parameters: kernel_size (int) – filter size. It should be odd and positive.
Return type: Tensor
Returns: 1D tensor with laplacian filter coefficients.

Shape:

Output: math:(text{kernel_size})

Examples

>>> get_laplacian_kernel1d(3)
tensor([ 1., -2.,  1.])
>>> get_laplacian_kernel1d(5)
tensor([ 1.,  1., -4.,  1.,  1.])

kornia.filters.get_laplacian_kernel2d(kernel_size)[source]#

Function that returns Gaussian filter matrix coefficients.

Parameters: kernel_size (int) – filter size should be odd.
Return type: Tensor
Returns: 2D tensor with laplacian filter matrix coefficients.

Shape:

Output: \((\text{kernel_size}_x, \text{kernel_size}_y)\)

Examples

>>> get_laplacian_kernel2d(3)
tensor([[ 1.,  1.,  1.],
        [ 1., -8.,  1.],
        [ 1.,  1.,  1.]])
>>> get_laplacian_kernel2d(5)
tensor([[  1.,   1.,   1.,   1.,   1.],
        [  1.,   1.,   1.,   1.,   1.],
        [  1.,   1., -24.,   1.,   1.],
        [  1.,   1.,   1.,   1.,   1.],
        [  1.,   1.,   1.,   1.,   1.]])

kornia.filters.get_motion_kernel2d(kernel_size, angle, direction=0.0, mode='nearest')[source]#

Return 2D motion blur filter.

Parameters

kernel_size (int) – motion kernel width and height. It should be odd and positive.
angle (Union[Tensor, float]) – angle of the motion blur in degrees (anti-clockwise rotation).
direction (Union[Tensor, float], optional) – forward/backward direction of the motion blur. Lower values towards -1.0 will point the motion blur towards the back (with angle provided via angle), while higher values towards 1.0 will point the motion blur forward. A value of 0.0 leads to a uniformly (but still angled) motion blur. Default: 0.0
mode (str, optional) – interpolation mode for rotating the kernel. 'bilinear' or 'nearest'. Default: 'nearest'

Return type

Tensor

Returns

The motion blur kernel of shape \((B, k_\text{size}, k_\text{size})\).

Examples

>>> get_motion_kernel2d(5, 0., 0.)
tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
         [0.2000, 0.2000, 0.2000, 0.2000, 0.2000],
         [0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]])

>>> get_motion_kernel2d(3, 215., -0.5)
tensor([[[0.0000, 0.0000, 0.1667],
         [0.0000, 0.3333, 0.0000],
         [0.5000, 0.0000, 0.0000]]])

Module#

class kornia.filters.BlurPool2D(kernel_size, stride=2)[source]#

Compute blur (anti-aliasing) and downsample a given feature map.

See [Zha19] for more details.

Parameters

kernel_size (int) – the kernel size for max pooling.
stride (int, optional) – stride for pooling. Default: 2

Shape:

Input: \((B, C, H, W)\)
Output: \((N, C, H_{out}, W_{out})\), where

\[H_{out} = \left\lfloor\frac{H_{in} + 2 \times \text{kernel\_size//2}[0] - \text{kernel\_size}[0]}{\text{stride}[0]} + 1\right\rfloor\]

\[W_{out} = \left\lfloor\frac{W_{in} + 2 \times \text{kernel\_size//2}[1] - \text{kernel\_size}[1]}{\text{stride}[1]} + 1\right\rfloor\]

Examples

>>> from kornia.filters.blur_pool import BlurPool2D
>>> input = torch.eye(5)[None, None]
>>> bp = BlurPool2D(kernel_size=3, stride=2)
>>> bp(input)
tensor([[[[0.3125, 0.0625, 0.0000],
          [0.0625, 0.3750, 0.0625],
          [0.0000, 0.0625, 0.3125]]]])

class kornia.filters.BoxBlur(kernel_size, border_type='reflect', normalized=True)[source]#

Blur an image using the box filter.

The function smooths an image using the kernel:

Parameters

kernel_size (Tuple[int, int]) – the blurring kernel size.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'.
normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True

Returns

the blurred input tensor.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Example

>>> input = torch.rand(2, 4, 5, 7)
>>> blur = BoxBlur((3, 3))
>>> output = blur(input)  # 2x4x5x7
>>> output.shape
torch.Size([2, 4, 5, 7])

class kornia.filters.MaxBlurPool2D(kernel_size, stride=2, max_pool_size=2, ceil_mode=False)[source]#

Compute pools and blurs and downsample a given feature map.

Equivalent to `nn.Sequential(nn.MaxPool2d(...), BlurPool2D(...))`

See [Zha19] for more details.

Parameters

kernel_size (int) – the kernel size for max pooling.
stride (int, optional) – stride for pooling. Default: 2
max_pool_size (int, optional) – the kernel size for max pooling. Default: 2
ceil_mode (bool, optional) – should be true to match output size of conv2d with same kernel size. Default: False

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H / stride, W / stride)\)

Returns: the transformed tensor.
Return type: torch.Tensor

Examples

>>> import torch.nn as nn
>>> from kornia.filters.blur_pool import BlurPool2D
>>> input = torch.eye(5)[None, None]
>>> mbp = MaxBlurPool2D(kernel_size=3, stride=2, max_pool_size=2, ceil_mode=False)
>>> mbp(input)
tensor([[[[0.5625, 0.3125],
          [0.3125, 0.8750]]]])
>>> seq = nn.Sequential(nn.MaxPool2d(kernel_size=2, stride=1), BlurPool2D(kernel_size=3, stride=2))
>>> seq(input)
tensor([[[[0.5625, 0.3125],
          [0.3125, 0.8750]]]])

class kornia.filters.MedianBlur(kernel_size)[source]#

Blur an image using the median filter.

Parameters: kernel_size (Tuple[int, int]) – the blurring kernel size.
Returns: the blurred input tensor.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Example

>>> input = torch.rand(2, 4, 5, 7)
>>> blur = MedianBlur((3, 3))
>>> output = blur(input)
>>> output.shape
torch.Size([2, 4, 5, 7])

class kornia.filters.GaussianBlur2d(kernel_size, sigma, border_type='reflect', separable=True)[source]#

Create an operator that blurs a tensor using a Gaussian filter.

The operator smooths the given tensor with a gaussian kernel by convolving it to each channel. It supports batched operation.

Parameters

kernel_size (Tuple[int, int]) – the size of the kernel.
sigma (Tuple[float, float]) – the standard deviation of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'.
separable (bool, optional) – run as composition of two 1d-convolutions. Default: True

Returns

the blurred tensor.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Examples:

>>> input = torch.rand(2, 4, 5, 5)
>>> gauss = GaussianBlur2d((3, 3), (1.5, 1.5))
>>> output = gauss(input)  # 2x4x5x5
>>> output.shape
torch.Size([2, 4, 5, 5])

class kornia.filters.Laplacian(kernel_size, border_type='reflect', normalized=True)[source]#

Create an operator that returns a tensor using a Laplacian filter.

The operator smooths the given tensor with a laplacian kernel by convolving it to each channel. It supports batched operation.

Parameters

kernel_size (int) – the size of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'
normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Examples

>>> input = torch.rand(2, 4, 5, 5)
>>> laplace = Laplacian(5)
>>> output = laplace(input)
>>> output.shape
torch.Size([2, 4, 5, 5])

class kornia.filters.Sobel(normalized=True, eps=1e-06)[source]#

Compute the Sobel operator and returns the magnitude per channel.

Parameters

normalized (bool, optional) – if True, L1 norm of the kernel is set to 1. Default: True
eps (float, optional) – regularization number to avoid NaN during backprop. Default: 1e-06

Returns

the sobel edge gradient magnitudes map.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Examples

>>> input = torch.rand(1, 3, 4, 4)
>>> output = Sobel()(input)  # 1x3x4x4

class kornia.filters.Canny(low_threshold=0.1, high_threshold=0.2, kernel_size=(5, 5), sigma=(1, 1), hysteresis=True, eps=1e-06)[source]#

Module that finds edges of the input image and filters them using the Canny algorithm.

Parameters

input – input image tensor with shape \((B,C,H,W)\).
low_threshold (float, optional) – lower threshold for the hysteresis procedure. Default: 0.1
high_threshold (float, optional) – upper threshold for the hysteresis procedure. Default: 0.2
kernel_size (Tuple[int, int], optional) – the size of the kernel for the gaussian blur. Default: (5, 5)
sigma (Tuple[float, float], optional) – the standard deviation of the kernel for the gaussian blur. Default: (1, 1)
hysteresis (bool, optional) – if True, applies the hysteresis edge tracking. Otherwise, the edges are divided between weak (0.5) and strong (1) edges. Default: True
eps (float, optional) – regularization number to avoid NaN during backprop. Default: 1e-06

Returns

the canny edge magnitudes map, shape of \((B,1,H,W)\).
the canny edge detection filtered by thresholds and hysteresis, shape of \((B,1,H,W)\).

Example

>>> input = torch.rand(5, 3, 4, 4)
>>> magnitude, edges = Canny()(input)  # 5x3x4x4
>>> magnitude.shape
torch.Size([5, 1, 4, 4])
>>> edges.shape
torch.Size([5, 1, 4, 4])

class kornia.filters.SpatialGradient(mode='sobel', order=1, normalized=True)[source]#

Compute the first order image derivative in both x and y using a Sobel operator.

Parameters

mode (str, optional) – derivatives modality, can be: sobel or diff. Default: 'sobel'
order (int, optional) – the order of the derivatives. Default: 1
normalized (bool, optional) – whether the output is normalized. Default: True

Returns

the sobel edges of the input feature map.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, 2, H, W)\)

Examples

>>> input = torch.rand(1, 3, 4, 4)
>>> output = SpatialGradient()(input)  # 1x3x2x4x4

class kornia.filters.SpatialGradient3d(mode='diff', order=1)[source]#

Compute the first and second order volume derivative in x, y and d using a diff operator.

Parameters

mode (str, optional) – derivatives modality, can be: sobel or diff. Default: 'diff'
order (int, optional) – the order of the derivatives. Default: 1

Returns

the spatial gradients of the input feature map.

Shape:

Input: \((B, C, D, H, W)\). D, H, W are spatial dimensions, gradient is calculated w.r.t to them.
Output: \((B, C, 3, D, H, W)\) or \((B, C, 6, D, H, W)\)

Examples

>>> input = torch.rand(1, 4, 2, 4, 4)
>>> output = SpatialGradient3d()(input)
>>> output.shape
torch.Size([1, 4, 3, 2, 4, 4])

class kornia.filters.MotionBlur(kernel_size, angle, direction, border_type='constant')[source]#

Blur 2D images (4D tensor) using the motion filter.

Parameters

kernel_size (int) – motion kernel width and height. It should be odd and positive.
angle (float) – angle of the motion blur in degrees (anti-clockwise rotation).
direction (float) – forward/backward direction of the motion blur. Lower values towards -1.0 will point the motion blur towards the back (with angle provided via angle), while higher values towards 1.0 will point the motion blur forward. A value of 0.0 leads to a uniformly (but still angled) motion blur.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'constant'

Returns

the blurred input tensor.

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Examples

>>> input = torch.rand(2, 4, 5, 7)
>>> motion_blur = MotionBlur(3, 35., 0.5)
>>> output = motion_blur(input)  # 2x4x5x7

class kornia.filters.UnsharpMask(kernel_size, sigma, border_type='reflect')[source]#

Create an operator that sharpens image with: out = 2 * image - gaussian_blur2d(image).

Parameters

kernel_size (Tuple[int, int]) – the size of the kernel.
sigma (Tuple[float, float]) – the standard deviation of the kernel.
border_type (str, optional) – the padding mode to be applied before convolving. The expected modes are: 'constant', 'reflect', 'replicate' or 'circular'. Default: 'reflect'

Returns

the sharpened tensor with shape \((B,C,H,W)\).

Shape:

Input: \((B, C, H, W)\)
Output: \((B, C, H, W)\)

Note

See a working example here.

Examples

>>> input = torch.rand(2, 4, 5, 5)
>>> sharpen = UnsharpMask((3, 3), (1.5, 1.5))
>>> output = sharpen(input)
>>> output.shape
torch.Size([2, 4, 5, 5])

kornia.filters#

Blurring#

Edge detection#

Filtering API#

Kernels#

Module#

Interactive Demo#