kornia.geometry.liegroup#

The Lie group encompasses the concepts of group and smooth manifold in a unique body.

A group is a non-empty set with an operation that satisfies the following constraints: the operation is associative, has an identity element, and every element of the set has an inverse element.

See more: Group

A Lie group \(G\) is a smooth manifold whose elements satisfy the group axioms.You can visualize the idea of manifold like a curved, smooth (hyper)-surface, with no edges or spikes, embedded in a space of higher dimension.

See more: Manifold

In robotics, we say that our state vector evolves on this surface, that is, the manifold describes or is defined by the constraints imposed on the state.

lie algebra#

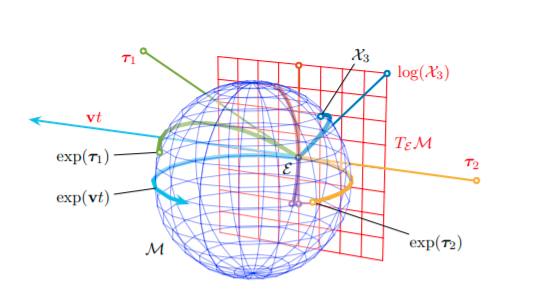
If \(M\) is the manifold that represents a lie group, the tangent space at the identity is called the Lie algebra of \(M\). The Lie algebra \(m\) is a vector space. As such, its elements can be identified with vectors in \(R^d\), whose dimension \(d\) is the number of degrees of freedom of \(M\). For example \(d\) would be 3 in the case of lie group \(SO3\)

lie group and lie algebra#

Every Lie group has an associated Lie algebra. We relate the Lie group with its Lie algebra through the following facts

The Lie algebra \(m\) is a vector space. As such, its elements can be identified with vectors in \(R^d\), whose dimension \(d\) is the number of degrees of freedom of \(M\).
The exponential map, exp : \(m\) → \(M\), exactly converts elements of the Lie algebra into elements of the group. The log map is the inverse operation.

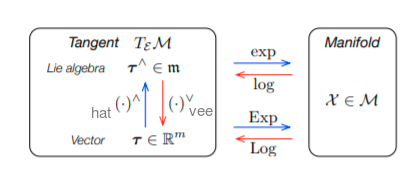
Reference: Micro lie theory

class kornia.geometry.liegroup.So3(q)#

Base class to represent the So3 group.

The SO(3) is the group of all rotations about the origin of three-dimensional Euclidean space \(R^3\) under the operation of composition. See more: https://en.wikipedia.org/wiki/3D_rotation_group

We internally represent the rotation by a unit quaternion.

Example

>>> q = Quaternion.identity()
>>> s = So3(q)
>>> s.q
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)

static Jl(vec)#

Alias for left jacobian.

Parameters:: vec (Tensor) – the input point of shape \((B, 3)\).
Return type:: Tensor

static Jr(vec)#

Alias for right jacobian.

Parameters:: vec (Tensor) – the input point of shape \((B, 3)\).
Return type:: Tensor

__init__(q)#

Constructor for the base class.

Internally represented by a unit quaternion q.

Parameters:: data – Quaternion with the shape of \((B, 4)\).

Example

>>> data = torch.ones((2, 4))
>>> q = Quaternion(data)
>>> So3(q)
Parameter containing:
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.]], requires_grad=True)

__mul__(right)#

Compose two So3 transformations.

Parameters:: right (So3) – the other So3 transformation.
Return type:: So3
Returns:: The resulting So3 transformation.

__repr__()#

Return repr(self).

Return type:: str

adjoint()#

Returns the adjoint matrix of shape \((B, 3, 3)\).

Return type:: Tensor

Example

>>> s = So3.identity()
>>> s.adjoint()
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]], grad_fn=<StackBackward0>)

static exp(v)#

Converts elements of lie algebra to elements of lie group.

See more: https://vision.in.tum.de/_media/members/demmeln/nurlanov2021so3log.pdf

Parameters:: v (Tensor) – vector of shape \((B,3)\).
Return type:: So3

Example

>>> v = torch.zeros((2, 3))
>>> s = So3.exp(v)
>>> s
Parameter containing:
tensor([[1., 0., 0., 0.],
        [1., 0., 0., 0.]], requires_grad=True)

classmethod from_matrix(matrix)#

Create So3 from a rotation matrix.

Parameters:: matrix (Tensor) – the rotation matrix to convert of shape \((B,3,3)\).
Return type:: So3

Example

>>> m = torch.eye(3)
>>> s = So3.from_matrix(m)
>>> s
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)

classmethod from_wxyz(wxyz)#

Create So3 from a tensor representing a quaternion.

Parameters:: wxyz (Tensor) – the quaternion to convert of shape \((B,4)\).
Return type:: So3

Example

>>> q = torch.tensor([1., 0., 0., 0.])
>>> s = So3.from_wxyz(q)
>>> s
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)

static hat(v)#

Converts elements from vector space to lie algebra. Returns matrix of shape \((B,3,3)\).

Parameters:: v (Vector3 | Tensor) – Vector3 or tensor of shape \((B,3)\).
Return type:: Tensor

Example

>>> v = torch.ones((1,3))
>>> m = So3.hat(v)
>>> m
tensor([[[ 0., -1.,  1.],
         [ 1.,  0., -1.],
         [-1.,  1.,  0.]]])

classmethod identity(batch_size=None, device=None, dtype=None)#

Create a So3 group representing an identity rotation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: So3

Example

>>> s = So3.identity()
>>> s
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)

>>> s = So3.identity(batch_size=2)
>>> s
Parameter containing:
tensor([[1., 0., 0., 0.],
        [1., 0., 0., 0.]], requires_grad=True)

inverse()#

Returns the inverse transformation.

Return type:: So3

Example

>>> s = So3.identity()
>>> s.inverse()
Parameter containing:
tensor([1., -0., -0., -0.], requires_grad=True)

static left_jacobian(vec)#

Computes the left Jacobian of So3.

Parameters:: vec (Tensor) – the input point of shape \((B, 3)\).
Return type:: Tensor

Example

>>> vec = torch.tensor([1., 2., 3.])
>>> So3.left_jacobian(vec)
tensor([[-0.0687, -0.2267,  0.5074],
        [ 0.5556,  0.1779,  0.3629],
        [-0.0141,  0.6236,  0.5890]])

log()#

Converts elements of lie group to elements of lie algebra.

Return type:: Tensor

Example

>>> data = torch.ones((2, 4))
>>> q = Quaternion(data)
>>> So3(q).log()
tensor([[0., 0., 0.],
        [0., 0., 0.]], grad_fn=<WhereBackward0>)

matrix()#

Convert the quaternion to a rotation matrix of shape \((B,3,3)\).

The matrix is of the form: :rtype: Tensor

\[\begin{split}\begin{bmatrix} 1-2y^2-2z^2 & 2xy-2zw & 2xy+2yw \\ 2xy+2zw & 1-2x^2-2z^2 & 2yz-2xw \\ 2xz-2yw & 2yz+2xw & 1-2x^2-2y^2\end{bmatrix}\end{split}\]

Example

>>> s = So3.identity()
>>> m = s.matrix()
>>> m
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]], grad_fn=<StackBackward0>)

property q: Quaternion#: Return the underlying data with shape \((B,4)\).

classmethod random(batch_size=None, device=None, dtype=None)#

Create a So3 group representing a random rotation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: So3

Example

>>> s = So3.random()
>>> s = So3.random(batch_size=3)

static right_jacobian(vec)#

Computes the right Jacobian of So3.

Parameters:: vec (Tensor) – the input point of shape \((B, 3)\).
Return type:: Tensor

Example

>>> vec = torch.tensor([1., 2., 3.])
>>> So3.right_jacobian(vec)
tensor([[-0.0687,  0.5556, -0.0141],
        [-0.2267,  0.1779,  0.6236],
        [ 0.5074,  0.3629,  0.5890]])

classmethod rot_x(x)#

Construct a x-axis rotation.

Parameters:: x (Tensor) – the x-axis rotation angle.
Return type:: So3

classmethod rot_y(y)#

Construct a z-axis rotation.

Parameters:: y (Tensor) – the y-axis rotation angle.
Return type:: So3

classmethod rot_z(z)#

Construct a z-axis rotation.

Parameters:: z (Tensor) – the z-axis rotation angle.
Return type:: So3

static vee(omega)#

Converts elements from lie algebra to vector space. Returns vector of shape \((B,3)\).

\[\begin{split}omega = \begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0\end{bmatrix}\end{split}\]

Parameters:: omega (Tensor) – 3x3-matrix representing lie algebra.
Return type:: Tensor

Example

>>> v = torch.ones((1,3))
>>> omega = So3.hat(v)
>>> So3.vee(omega)
tensor([[1., 1., 1.]])

class kornia.geometry.liegroup.Se3(rotation, translation)#

Base class to represent the Se3 group.

The SE(3) is the group of rigid body transformations about the origin of three-dimensional Euclidean space \(R^3\) under the operation of composition. See more: https://ingmec.ual.es/~jlblanco/papers/jlblanco2010geometry3D_techrep.pdf

Example

>>> q = Quaternion.identity()
>>> s = Se3(q, torch.ones(3))
>>> s.r
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)
>>> s.t
Parameter containing:
tensor([1., 1., 1.], requires_grad=True)

__init__(rotation, translation)#

Constructor for the base class.

Internally represented by a unit quaternion q and a translation 3-vector.

Parameters:

rotation (Quaternion | So3) – So3 group encompassing a rotation.
translation (Vector3 | Tensor) – Vector3 or translation tensor with the shape of \((B, 3)\).

Example

>>> from kornia.geometry.quaternion import Quaternion
>>> q = Quaternion.identity(batch_size=1)
>>> s = Se3(q, torch.ones((1, 3)))
>>> s.r
Parameter containing:
tensor([[1., 0., 0., 0.]], requires_grad=True)
>>> s.t
Parameter containing:
tensor([[1., 1., 1.]], requires_grad=True)

__mul__(right)#

Compose two Se3 transformations.

Parameters:: right (Se3) – the other Se3 transformation.
Return type:: Se3 | Vector3 | Tensor
Returns:: The resulting Se3 transformation.

__repr__()#

Return repr(self).

Return type:: str

adjoint()#

Returns the adjoint matrix of shape \((B, 6, 6)\).

Return type:: Tensor

Example

>>> s = Se3.identity()
>>> s.adjoint()
tensor([[1., 0., 0., 0., 0., 0.],
        [0., 1., 0., 0., 0., 0.],
        [0., 0., 1., 0., 0., 0.],
        [0., 0., 0., 1., 0., 0.],
        [0., 0., 0., 0., 1., 0.],
        [0., 0., 0., 0., 0., 1.]], grad_fn=<CatBackward0>)

static exp(v)#

Converts elements of lie algebra to elements of lie group.

Parameters:: v (Tensor) – vector of shape \((B, 6)\).
Return type:: Se3

Example

>>> v = torch.zeros((1, 6))
>>> s = Se3.exp(v)
>>> s.r
Parameter containing:
tensor([[1., 0., 0., 0.]], requires_grad=True)
>>> s.t
Parameter containing:
tensor([[0., 0., 0.]], requires_grad=True)

classmethod from_matrix(matrix)#

Create a Se3 group from a matrix.

Parameters:: matrix (Tensor) – tensor of shape \((B, 4, 4)\).
Return type:: Se3

Example

>>> s = Se3.from_matrix(torch.eye(4))
>>> s.r
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)
>>> s.t
Parameter containing:
tensor([0., 0., 0.], requires_grad=True)

classmethod from_qxyz(qxyz)#

Create a Se3 group a quaternion and translation vector.

Parameters:: qxyz (Tensor) – tensor of shape \((B, 7)\).
Return type:: Se3

Example

>>> qxyz = torch.tensor([1., 2., 3., 0., 0., 0., 1.])
>>> s = Se3.from_qxyz(qxyz)
>>> s.r
Parameter containing:
tensor([1., 2., 3., 0.], requires_grad=True)
>>> s.t
x: 0.0
y: 0.0
z: 1.0

static hat(v)#

Converts elements from vector space to lie algebra.

Parameters:: v (Tensor) – vector of shape \((B, 6)\).
Return type:: Tensor
Returns:: matrix of shape \((B, 4, 4)\).

Example

>>> v = torch.ones((1, 6))
>>> m = Se3.hat(v)
>>> m
tensor([[[ 0., -1.,  1.,  1.],
         [ 1.,  0., -1.,  1.],
         [-1.,  1.,  0.,  1.],
         [ 0.,  0.,  0.,  0.]]])

classmethod identity(batch_size=None, device=None, dtype=None)#

Create a Se3 group representing an identity rotation and zero translation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: Se3

Example

>>> s = Se3.identity()
>>> s.r
Parameter containing:
tensor([1., 0., 0., 0.], requires_grad=True)
>>> s.t
x: 0.0
y: 0.0
z: 0.0

inverse()#

Returns the inverse transformation.

Return type:: Se3

Example

>>> s = Se3(So3.identity(), torch.ones(3))
>>> s_inv = s.inverse()
>>> s_inv.r
Parameter containing:
tensor([1., -0., -0., -0.], requires_grad=True)
>>> s_inv.t
Parameter containing:
tensor([-1., -1., -1.], requires_grad=True)

log()#

Converts elements of lie group to elements of lie algebra.

Return type:: Tensor

Example

>>> from kornia.geometry.quaternion import Quaternion
>>> q = Quaternion.identity()
>>> Se3(q, torch.zeros(3)).log()
tensor([0., 0., 0., 0., 0., 0.], grad_fn=<CatBackward0>)

matrix()#

Returns the matrix representation of shape \((B, 4, 4)\).

Return type:: Tensor

Example

>>> s = Se3(So3.identity(), torch.ones(3))
>>> s.matrix()
tensor([[1., 0., 0., 1.],
        [0., 1., 0., 1.],
        [0., 0., 1., 1.],
        [0., 0., 0., 1.]], grad_fn=<CopySlices>)

property quaternion: Quaternion#: Return the underlying rotation(Quaternion).

property r: So3#: Return the underlying rotation(So3).

classmethod random(batch_size=None, device=None, dtype=None)#

Create a Se3 group representing a random transformation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: Se3

Example

>>> s = Se3.random()
>>> s = Se3.random(batch_size=3)

classmethod rot_x(x)#

Construct a x-axis rotation.

Parameters:: x (Tensor) – the x-axis rotation angle.
Return type:: Se3

classmethod rot_y(y)#

Construct a y-axis rotation.

Parameters:: y (Tensor) – the y-axis rotation angle.
Return type:: Se3

classmethod rot_z(z)#

Construct a z-axis rotation.

Parameters:: z (Tensor) – the z-axis rotation angle.
Return type:: Se3

property rotation: So3#: Return the underlying rotation(So3).

property so3: So3#: Return the underlying rotation(So3).

property t: Vector3 | Tensor#: Return the underlying translation vector of shape \((B,3)\).

classmethod trans(x, y, z)#

Construct a translation only Se3 instance.

Parameters:

x (Tensor) – the x-axis translation.
y (Tensor) – the y-axis translation.
z (Tensor) – the z-axis translation.

Return type:

Se3

classmethod trans_x(x)#

Construct a x-axis translation.

Parameters:: x (Tensor) – the x-axis translation.
Return type:: Se3

classmethod trans_y(y)#

Construct a y-axis translation.

Parameters:: y (Tensor) – the y-axis translation.
Return type:: Se3

classmethod trans_z(z)#

Construct a z-axis translation.

Parameters:: z (Tensor) – the z-axis translation.
Return type:: Se3

property translation: Vector3 | Tensor#: Return the underlying translation vector of shape \((B,3)\).

static vee(omega)#

Converts elements from lie algebra to vector space.

Parameters:: omega (Tensor) – 4x4-matrix representing lie algebra of shape \((B,4,4)\).
Return type:: Tensor
Returns:: vector of shape \((B,6)\).

Example

>>> v = torch.ones((1, 6))
>>> omega_hat = Se3.hat(v)
>>> Se3.vee(omega_hat)
tensor([[1., 1., 1., 1., 1., 1.]])

class kornia.geometry.liegroup.So2(z)#

Base class to represent the So2 group.

The SO(2) is the group of all rotations about the origin of two-dimensional Euclidean space \(R^2\) under the operation of composition. See more: https://en.wikipedia.org/wiki/Orthogonal_group#Special_orthogonal_group

We internally represent the rotation by a complex number.

Example

>>> real = torch.tensor([1.0])
>>> imag = torch.tensor([2.0])
>>> So2(torch.complex(real, imag))
Parameter containing:
tensor([1.+2.j], requires_grad=True)

__init__(z)#

Constructor for the base class.

Internally represented by complex number z.

Parameters:: z (Tensor) – Complex number with the shape of \((B, 1)\) or \((B)\).

Example

>>> real = torch.tensor(1.0)
>>> imag = torch.tensor(2.0)
>>> So2(torch.complex(real, imag)).z
Parameter containing:
tensor(1.+2.j, requires_grad=True)

__mul__(right)#

Performs a left-multiplication either rotation concatenation or point-transform.

Parameters:: right (So2 | Tensor) – the other So2 transformation.
Return type:: So2 | Tensor
Returns:: The resulting So2 transformation.

__repr__()#

Return repr(self).

Return type:: str

adjoint()#

Returns the adjoint matrix of shape \((B, 2, 2)\).

Return type:: Tensor

Example

>>> s = So2.identity()
>>> s.adjoint()
tensor([[1., -0.],
        [0., 1.]], grad_fn=<StackBackward0>)

static exp(theta)#

Converts elements of lie algebra to elements of lie group.

Parameters:: theta (Tensor) – angle in radians of shape \((B, 1)\) or \((B)\).
Return type:: So2

Example

>>> v = torch.tensor([3.1415/2])
>>> s = So2.exp(v)
>>> s
Parameter containing:
tensor([4.6329e-05+1.j], requires_grad=True)

classmethod from_matrix(matrix)#

Create So2 from a rotation matrix.

Parameters:: matrix (Tensor) – the rotation matrix to convert of shape \((B, 2, 2)\).
Return type:: So2

Example

>>> m = torch.eye(2)
>>> s = So2.from_matrix(m)
>>> s.z
Parameter containing:
tensor(1.+0.j, requires_grad=True)

static hat(theta)#

Converts elements from vector space to lie algebra. Returns matrix of shape \((B, 2, 2)\).

Parameters:: theta (Tensor) – angle in radians of shape \((B)\).
Return type:: Tensor

Example

>>> theta = torch.tensor(3.1415/2)
>>> So2.hat(theta)
tensor([[0.0000, 1.5707],
        [1.5707, 0.0000]])

classmethod identity(batch_size=None, device=None, dtype=None)#

Create a So2 group representing an identity rotation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: So2

Example

>>> s = So2.identity(batch_size=2)
>>> s
Parameter containing:
tensor([1.+0.j, 1.+0.j], requires_grad=True)

inverse()#

Returns the inverse transformation.

Return type:: So2

Example

>>> s = So2.identity()
>>> s.inverse().z
Parameter containing:
tensor(1.+0.j, requires_grad=True)

log()#

Converts elements of lie group to elements of lie algebra.

Return type:: Tensor

Example

>>> real = torch.tensor([1.0])
>>> imag = torch.tensor([3.0])
>>> So2(torch.complex(real, imag)).log()
tensor([1.2490], grad_fn=<Atan2Backward0>)

matrix()#

Convert the complex number to a rotation matrix of shape \((B, 2, 2)\).

Return type:: Tensor

Example

>>> s = So2.identity()
>>> m = s.matrix()
>>> m
tensor([[1., -0.],
        [0., 1.]], grad_fn=<StackBackward0>)

classmethod random(batch_size=None, device=None, dtype=None)#

Create a So2 group representing a random rotation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: So2

Example

>>> s = So2.random()
>>> s = So2.random(batch_size=3)

static vee(omega)#

Converts elements from lie algebra to vector space. Returns vector of shape \((B,)\).

Parameters:: omega (Tensor) – 2x2-matrix representing lie algebra.
Return type:: Tensor

Example

>>> v = torch.ones(3)
>>> omega = So2.hat(v)
>>> So2.vee(omega)
tensor([1., 1., 1.])

property z: Tensor#: Return the underlying data with shape \((B, 1)\).

class kornia.geometry.liegroup.Se2(rotation, translation)#

Base class to represent the Se2 group.

The SE(2) is the group of rigid body transformations about the origin of two-dimensional Euclidean space \(R^2\) under the operation of composition. See more:

Example

>>> so2 = So2.identity(1)
>>> t = torch.ones((1, 2))
>>> se2 = Se2(so2, t)
>>> se2
rotation: Parameter containing:
tensor([1.+0.j], requires_grad=True)
translation: Parameter containing:
tensor([[1., 1.]], requires_grad=True)

__init__(rotation, translation)#

Constructor for the base class.

Internally represented by a complex number z and a translation 2-vector.

Parameters:

rotation (So2) – So2 group encompassing a rotation.
translation (Vector2 | Tensor) – translation vector with the shape of \((B, 2)\).

Example

>>> so2 = So2.identity(1)
>>> t = torch.ones((1, 2))
>>> se2 = Se2(so2, t)
>>> se2
rotation: Parameter containing:
tensor([1.+0.j], requires_grad=True)
translation: Parameter containing:
tensor([[1., 1.]], requires_grad=True)

__mul__(right)#

Compose two Se2 transformations.

Parameters:: right (Se2 | Tensor) – the other Se2 transformation.
Return type:: Se2 | Tensor
Returns:: The resulting Se2 transformation.

__repr__()#

Return repr(self).

Return type:: str

adjoint()#

Returns the adjoint matrix of shape \((B, 3, 3)\).

Return type:: Tensor

Example

>>> s = Se2.identity()
>>> s.adjoint()
tensor([[1., -0., 0.],
        [0., 1., -0.],
        [0., 0., 1.]], grad_fn=<CopySlices>)

static exp(v)#

Converts elements of lie algebra to elements of lie group.

Parameters:: v (Tensor) – vector of shape \((B, 3)\).
Return type:: Se2

Example

>>> v = torch.ones((1, 3))
>>> s = Se2.exp(v)
>>> s.r
Parameter containing:
tensor([0.5403+0.8415j], requires_grad=True)
>>> s.t
Parameter containing:
tensor([[0.3818, 1.3012]], requires_grad=True)

classmethod from_matrix(matrix)#

Create an Se2 group from a matrix.

Parameters:: matrix (Tensor) – tensor of shape \((B, 3, 3)\).
Return type:: Se2

Example

>>> s = Se2.from_matrix(torch.eye(3).repeat(2, 1, 1))
>>> s.r
Parameter containing:
tensor([1.+0.j, 1.+0.j], requires_grad=True)
>>> s.t
Parameter containing:
tensor([[0., 0.],
        [0., 0.]], requires_grad=True)

static hat(v)#

Converts elements from vector space to lie algebra. Returns matrix of shape \((B, 3, 3)\).

Parameters:: v (Tensor) – vector of shape:math:(B, 3).
Return type:: Tensor

Example

>>> theta = torch.tensor(3.1415/2)
>>> So2.hat(theta)
tensor([[0.0000, 1.5707],
        [1.5707, 0.0000]])

classmethod identity(batch_size=None, device=None, dtype=None)#

Create a Se2 group representing an identity rotation and zero translation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: Se2

Example

>>> s = Se2.identity(1)
>>> s.r
Parameter containing:
tensor([1.+0.j], requires_grad=True)
>>> s.t
x: tensor([0.])
y: tensor([0.])

inverse()#

Returns the inverse transformation.

Return type:: Se2

Example

>>> s = Se2(So2.identity(1), torch.ones(1,2))
>>> s_inv = s.inverse()
>>> s_inv.r
Parameter containing:
tensor([1.+0.j], requires_grad=True)
>>> s_inv.t
Parameter containing:
tensor([[-1., -1.]], requires_grad=True)

log()#

Converts elements of lie group to elements of lie algebra.

Return type:: Tensor

Example

>>> v = torch.ones((1, 3))
>>> s = Se2.exp(v).log()
>>> s
tensor([[1.0000, 1.0000, 1.0000]], grad_fn=<StackBackward0>)

matrix()#

Returns the matrix representation of shape \((B, 3, 3)\).

Return type:: Tensor

Example

>>> s = Se2(So2.identity(1), torch.ones(1, 2))
>>> s.matrix()
tensor([[[1., -0., 1.],
         [0., 1., 1.],
         [0., 0., 1.]]], grad_fn=<CopySlices>)

property r: So2#: Return the underlying rotation(So2).

classmethod random(batch_size=None, device=None, dtype=None)#

Create a Se2 group representing a random transformation.

Parameters:: batch_size (Optional[int], optional) – the batch size of the underlying data. Default: None
Return type:: Se2

Example

>>> s = Se2.random()
>>> s = Se2.random(batch_size=3)

property rotation: So2#: Return the underlying rotation(So2).

property so2: So2#: Return the underlying rotation(So2).

property t: Vector2 | Parameter#: Return the underlying translation vector of shape \((B,2)\).

classmethod trans(x, y)#

Construct a translation only Se2 instance.

Parameters:

x (Tensor) – the x-axis translation.
y (Tensor) – the y-axis translation.

Return type:

Se2

classmethod trans_x(x)#

Construct a x-axis translation.

Parameters:: x (Tensor) – the x-axis translation.
Return type:: Se2

classmethod trans_y(y)#

Construct a y-axis translation.

Parameters:: y (Tensor) – the y-axis translation.
Return type:: Se2

property translation: Vector2 | Parameter#: Return the underlying translation vector of shape \((B,2)\).

static vee(omega)#

Converts elements from lie algebra to vector space.

Parameters:: omega (Tensor) – 3x3-matrix representing lie algebra of shape \((B, 3, 3)\).
Return type:: Tensor
Returns:: vector of shape \((B, 3)\).

Example

>>> v = torch.ones(3)
>>> omega_hat = Se2.hat(v)
>>> Se2.vee(omega_hat)
tensor([1., 1., 1.])